Calculating Fractal Dimension

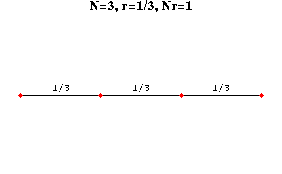
Consider a line segment divided into N equal pieces. Each of these N pieces can be thought of as a scaled version of the whole segment, with scaling ratio r=1/N. The relation between N and r is clearly Nr=1. For example, if N=3, then r=1/3 and Nr=(3)(1/3)=1. (See the figure generated by the cell below.)

Input := 

Clear[points,line,n]
points=ListPlot[{{0,0},{1/3,0},{2/3,0},{1,0}},
	PlotStyle->{Red,PointSize[.02]},Axes->False,
	DisplayFunction->Identity];
line=Graphics[Line[{{0,0},{1,0}}]];
Show[{line,
	   points,
	   Graphics[Table[
	   			  Text["1/3",{n,.01}],{n,1/6,5/6,1/3}]]},
	   PlotLabel->FontForm["N=3, r=1/3, Nr=1",
	 		{"Times-Bold",14}],
	 	PlotRange->{-.1,.1},
	 	DisplayFunction->$DisplayFunction]

Output =

-Graphics-

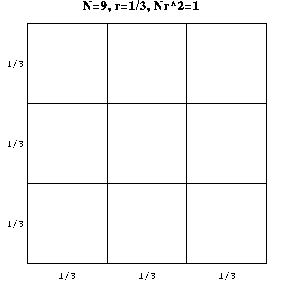
Now suppose the sides of a square are scaled by a factor r to produce N identical subsquares, each of which is a scaled version of the whole square. The relation between N and r in this case is Nr2=1. For example, if r=1/3, then N=9 and Nr2=(9)(1/9)=1. (See the figure generated by the cell below.)

Input := 

Clear[i,j,n,horizontal,vertical]
horizontal=Table[Graphics[Line[{{0,j},{1,j}}]],
	{j,0,1,1/3}];
vertical=Table[Graphics[Line[{{i,0},{i,1}}]],
	{i,0,1,1/3}];
Show[{
	  horizontal,
	  vertical,
	  Graphics[Table[
	  		Text["1/3",{-.05,n}],{n,1/6,5/6,1/3}]],
	  Graphics[Table[
	  		Text["1/3",{n,-.05}],{n,1/6,5/6,1/3}]]},
	  AspectRatio->1,
	  PlotLabel->FontForm["N=9, r=1/3, Nr^2=1",
	 		{"Times-Bold",14}]]

Output =

-Graphics-

Finally, if a cube is scaled in the x, y, and z directions by a factor r to produce N equal subcubes, then the relation is Nr3=1. For example, if r=1/3, then N=27 and Nr3=(27)(1/27)=1. (See the figure generated by the cell below.)

Input := 

Clear[i,j,k,n]
Show[{
	Table[Graphics3D[Cuboid[{i,j,k},
	{i+1/3,j+1/3,k+1/3}]],
	{i,0,2/3,1/3},{j,0,2/3,1/3},{k,0,2/3,1/3}],
	Graphics3D[Table[
		Text["1/3",{n,-.05,-.05}],{n,1/6,5/6,1/3}]],
	Graphics3D[Table[
		Text["1/3",{1.05,n,-.05}],{n,1/6,5/6,1/3}]],	
	Graphics3D[Table[
		Text["1/3",{-.05,-.05,n}],{n,1/6,5/6,1/3}]]},
	Boxed->False,
	PlotLabel->FontForm["N=27, r=1/3, Nr^3=1",
	 	{"Times-Bold",14}]]

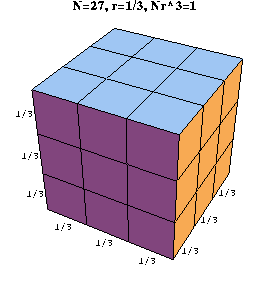
Output =

-Graphics3D-

The line, square, and cube above have integer dimensions of one, two, and three respectively. Notice that the dimensions of these objects show up as the exponent d in the relation Nrd=1, where N is the number of equal subunits and r is the scaling ratio. In general, if a given set is the union of N essentially disjoint copies of the original that are scaled by a constant factor r, then the value of d that satisfies the equation Nrd=1 is called the fractal dimension or similarity dimension of the set.

It turns out that there are configurations for which the value of d in Nrd=1 is not an integer. Such configurations are called self-similar fractals.

The explicit formula for d in terms or N and r is given by the cell below.

Input := 

Solve[n r^d==1,d]

Solve::ifun: 
   Warning: Inverse functions are being used
     by Solve, so some solutions may not be
     found.

Output =

           1
       Log[-]
           n
{{d -> ------}}
       Log[r]

The logarithm in the formula above can be taken with respect to any positive base different from 1. The following cell defines a function called dimension that takes the values of N and r as input and returns the value of d. This function will be used later in this notebook, so execute it now.

Input := 

Clear[dimension,d]
dimension[n_Integer?Positive,r_?Positive]:=
	Module[{d},
		d=Log[1/n]/Log[r]//N]